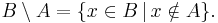Complement (set theory)

In set theory, a complement of a set A refers to things not in (that is, things outside of), A. The relative complement of A with respect to a set B, is the set of elements in B but not in A. When all sets under consideration are considered to be subsets of a given set U, the absolute complement of A is the set of all elements in U but not in A.

1 Relative complement
2 Logical complement
3 Absolute complement
4 Notation
5 Complements in various programming languages
6 See also
7 References

Relative complement

If A and B are sets, then the relative complement of A in B, also known as the set-theoretic difference of B and A, is the set of elements in B, but not in A.

The relative complement of A in B:
$A^c \cap B~~~~=~~~~B \setminus A$

The relative complement of A in B is denoted B ∖ A (sometimes written B − A, but this notation is ambiguous, as in some contexts it can be interpreted as the set of all b − a, where b is taken from B and a from A).

Formally

$B \setminus A = \{ x\in B \, | \, x \notin A \}.$

Examples:

{1,2,3} ∖ {2,3,4} = {1}
{2,3,4} ∖ {1,2,3} = {4}
If 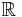$\mathbb{R}$ is the set of real numbers and 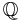$\mathbb{Q}$ is the set of rational numbers, then $\mathbb{R}\setminus\mathbb{Q}$ is the set of irrational numbers.

The following proposition lists some notable properties of relative complements in relation to the set-theoretic operations of union and intersection.

PROPOSITION 2: If A, B, and C are sets, then the following identities hold:

C ∖ (A ∩ B) = (C ∖ A)∪(C ∖ B)
C ∖ (A ∪ B) = (C ∖ A)∩(C ∖ B)
C ∖ (B ∖ A) = (A ∩ C)∪(C ∖ B)
(B ∖ A) ∩ C = (B ∩ C) ∖ A = B∩(C ∖ A)
(B ∖ A) ∪ C = (B ∪ C) ∖ (A ∖ C)
A ∖ A = Ø
Ø ∖ A = Ø
A ∖ Ø = A

Logical complement

A subset S of a set X with an inequality = has another complementary subset related to the relative complement called the logical complement and is defined as:

¬S = {x ∈ X | ∀y ∈ S ¬(x=y)}

Absolute complement

The complement of A in U:
$A^c~~~~=~~~~U \setminus A$

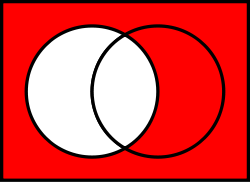
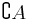If a universe U is defined, then the relative complement of A in U is called the absolute complement (or simply complement) of A, and is denoted by A^c or sometimes A′, also the same set often is denoted by $\complement_U A$ or $\complement A$ if U is fixed, that is:

A^c = U ∖ A.

For example, if the universe is the set of integers, then the complement of the set of odd numbers is the set of even numbers.

The following proposition lists some important properties of absolute complements in relation to the set-theoretic operations of union and intersection.

PROPOSITION 1: If A and B are subsets of a universe U, then the following identities hold:

De Morgan's laws:

(A ∪ B)^c = A^c ∩ B^c
(A ∩ B)^c = A^c ∪ B^c

Complement laws:

A ∪ A^c = U
A ∩ A^c = Ø
Ø^c = U
U^c = Ø
If A⊆B, then B^c⊆A^c (this follows from the equivalence of a conditional with its contrapositive)

Involution or double complement law:

A^c^c = A.

Relationships between relative and absolute complements:

A ∖ B = A ∩ B^c
(A ∖ B)^c = A^c ∪ B

The first two complement laws above shows that if A is a non-empty, proper subset of U, then {A, A^c} is a partition of U.

Notation

In the LaTeX typesetting language, the command \setminus is usually used for rendering a set difference symbol, which is similar to a backslash symbol. When rendered the \setminus command looks identical to \backslash except that it has a little more space in front and behind the slash, akin to the LaTeX sequence \mathbin{\backslash}. A variant \smallsetminus is available in the amssymb package.

Complements in various programming languages

Some programming languages allow for manipulation of sets as data structures, using these operators or functions to construct the difference of sets a and b:

Mathematica: Complement^[1]

MATLAB: setdiff^[2]

MathML: <apply xmlns="http://www.w3.org/1998/Math/MathML"> <setdiff/> <ci type="set">A</ci> <ci type="set">B</ci></apply>

Pascal: SetDifference := a - b;

Python: diff = a.difference(b)^[3]; diff = a - b^[3]

Java: diff = a.clone();; diff.removeAll(b);^[4]

C++: set_difference(a.begin(), a.end(), b.begin(), b.end(), result.begin());

.NET Framework: a.Except(b);

Haskell: a \\ b ^[5]

Common Lisp: set-difference, nset-difference^[6]

References

↑ Complement. Mathematica Documentation Center for version 6.0, updated in 2008. Accessed on March 7, 2008.
↑ Setdiff. MATLAB Function Reference for version 7.6, updated in 2008. Accessed on May 19, 2008.
↑ ^3.0 ^3.1 Set Types -- set, frozenset. Python Library Reference release 2.5, updated on September 19, 2006. Accessed on February 13, 2008.
↑ Set (Java 2 Platform SE 5.0). JavaTM 2 Platform Standard Edition 5.0 API Specification, updated in 2004. Accessed on February 13, 2008.
↑ Data.Set (Haskell)
↑ Common Lisp HyperSpec, Function set-difference, nset-difference. Accessed on September 8, 2009.